|
Solving an 8x8 Star Battle puzzleA tutorial by Krazydad
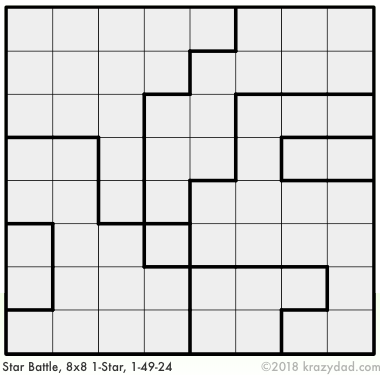
Here's how to solve a medium difficulty Star Battle puzzle. This is the puzzle I'm solving.
In these 8x8 puzzles, each row, column and bolded region must contain a single star. The stars can't touch each other, not even diagonally. So when you place a star, you can eliminate all the cells that immediately surround it, as well as the remaining cells on its row and column. 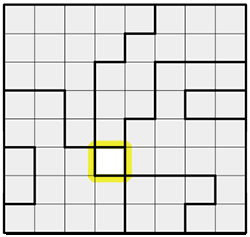
The first thing you'll notice is that there is a region that consists of a single cell. Those are freebies, and you won't encounter more than one per puzzle. So we'll put a star in it, then mark the surrounding (touching) cells, as well as the remaining cells in the row and column. Note that I'm using marks to indicate cells that can't contain a star -- the cells that I'm ruling out. In these puzzles, you'll typically make a lot of these marks.
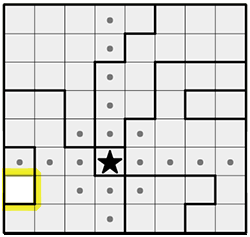
Our marks have eliminated one of the cells from the small region on the left, leaving a single remaining cell. So we'll fill that in too, and mark the row, column and surrounding cells.
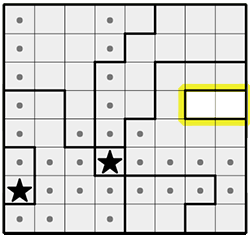
Now take a look at the small region I've highlighted. One of those two cells must contain a star. This has consequences. It means that none of the other cells in that row can contain a star, and it means that the two cells immediately above and below that region can't contain a star (because they are adjacent to both cells in the region, and would prevent a star from going in the region).
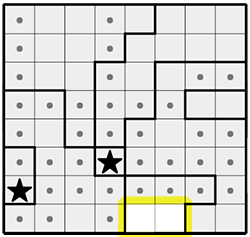
Now look at the two cells I've highlighted. These are the only remaining available cells from a 5-cell region. Again, one of these two cells must contain a star, so we can rule out the remaining cells on this row.
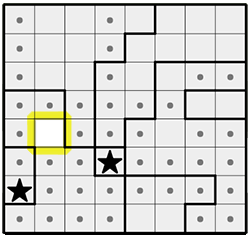
Now I've ruled out all but one cell from a larger region. Once I place that star, the rest of the puzzle is solved easily, using the above techniques.

Note that my 1-star puzzles are significantly easier my larger 10x10 2-star puzzles. Here's a longer tutorial for one of those.
Privacy Policy Contact Krazydad Discord server |