Advanced Strategies for Two Not Touch Puzzles

A tutorial by Krazydad

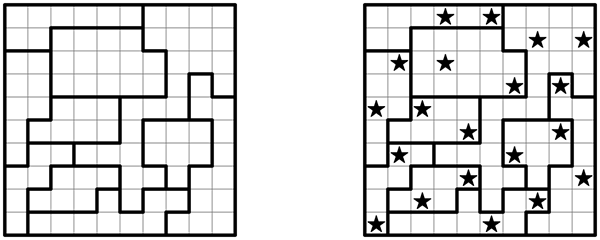
Here is a collection of advanced strategies for Two Not Touch (also known as Star Battle), partially based on correspondence I've received for my puzzles in The New York Times.

If you are new to these puzzles, go check out my Intro Tutorial before proceeding further; the Intermediate Tutorial has another fully-worked example that may help you get the hang of solving these.

NOTE: In this tutorial, I use the words square and cell interchangeably. The word container is used to refer to rows, columns, and bolded regions.

These first two rules have been informally covered in the previous tutorials, but I'll state them more formally here:

RULE OF FINISHED CONTAINERS

If a container has only one possible set of locations where you can place its remaining stars, place the stars there. If a container has all of its stars placed, then the rest of it can be eliminated.

This is the most basic rule of Two Not Touch, and is the only rule you need to solve the easiest puzzles. We've used it extensively in the previous two tutorials.

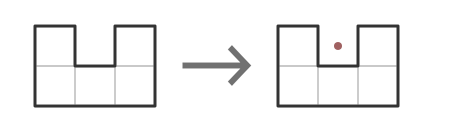
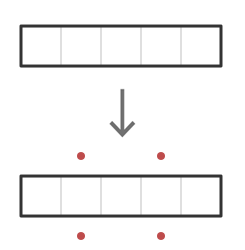
RULE OF NOSY NEIGHBORS

If a set of cells is known to contain one or more stars, any exterior square adjacent to all the cells of that set can be eliminated. After a time, you will begin to recognize patterns which are the result of this rule. For example, in the U-shaped region below, there is an exterior square that is adjacent to all the cells, and it can be eliminated as shown.

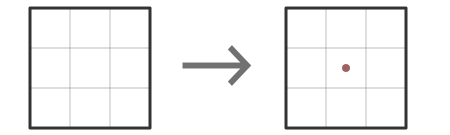
RULE OF SELFISH ROOMMATES

If a set of cells is known to contain two or more stars, any cell in the set adjacent to all other cells in the set can be eliminated. For example, if a container is a 3x3 block, the center cell can always be eliminated, because it is adjacent to all the other cells in the container.

The above two rules can be replaced by a single generalized rule:

RULE OF CROWDING

If any cell is adjacent to enough squares in a group of cells known to contain a star such that it prevents us from placing all remaining stars in that group, it can be eliminated.

For example, if there are 5 cells in a row that are known to contain two stars, there are two cells on either side that can't be used, because they prevent us from placing those stars.

RULE OF FOUR-SQUARES

In a N-star puzzle, if an unsolved region can be divided into N discrete sub-regions which each fit into a 2x2 area (a four-square), then each sub-region must contain exactly one star.

Note that Two Not Touch as published in The New York Times is a 2-star puzzle, so for these puzzles, look for regions that can be subdivided into two discrete four-square sub-regions.

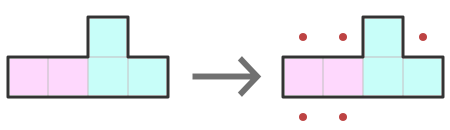
RULE OF CLUMPS

Divide each container into discrete clumps that must contain one star, using the four-square technique. If the number of clumps is equal to the count of remaining stars for that container, we can treat each clump as its own one-star container, applying the Rule of Crowding and the Rule of Finished Containers to them individually.

In the following example, I use the Rule of Clumps to split the region into two parts that each fit into a four-square. We can then use the Rule of Crowding to eliminate external squares that would crowd each of those sub-regions.

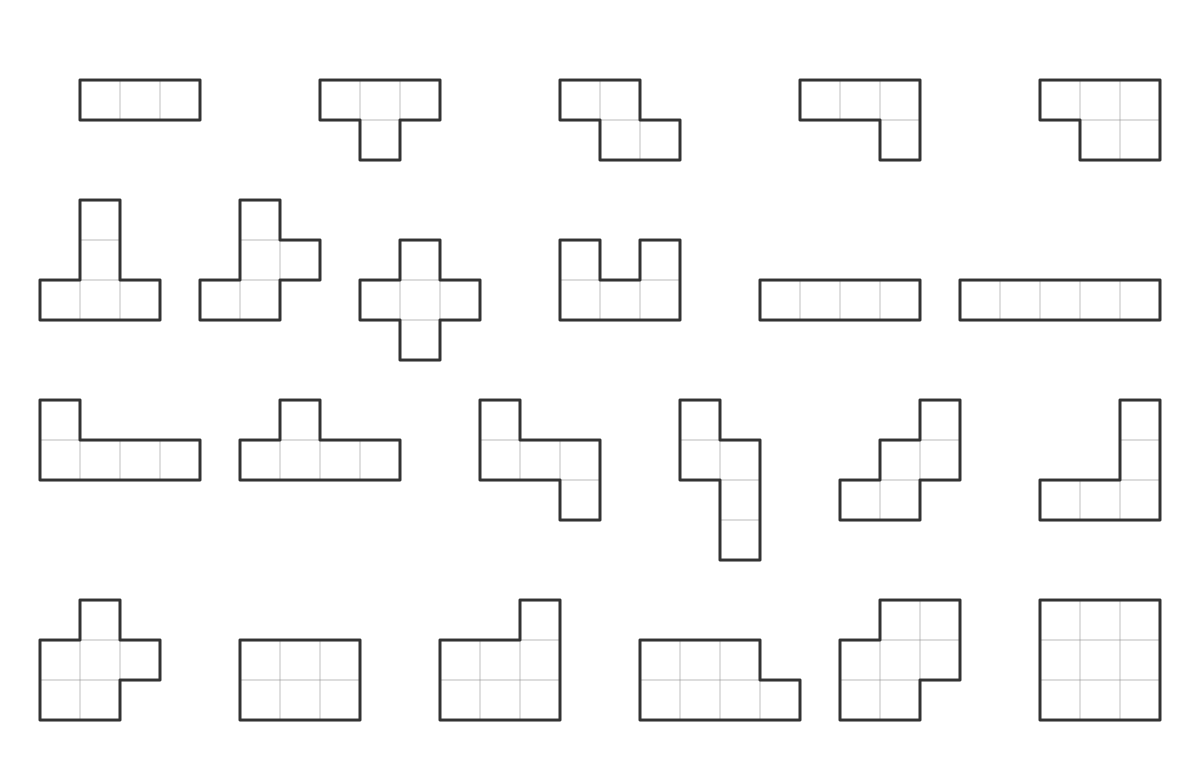
By combining each of the above rules, there are a lot of eliminations that can be made, especially around regions that are already small and crowded to begin with. Here are a number of common small shapes:

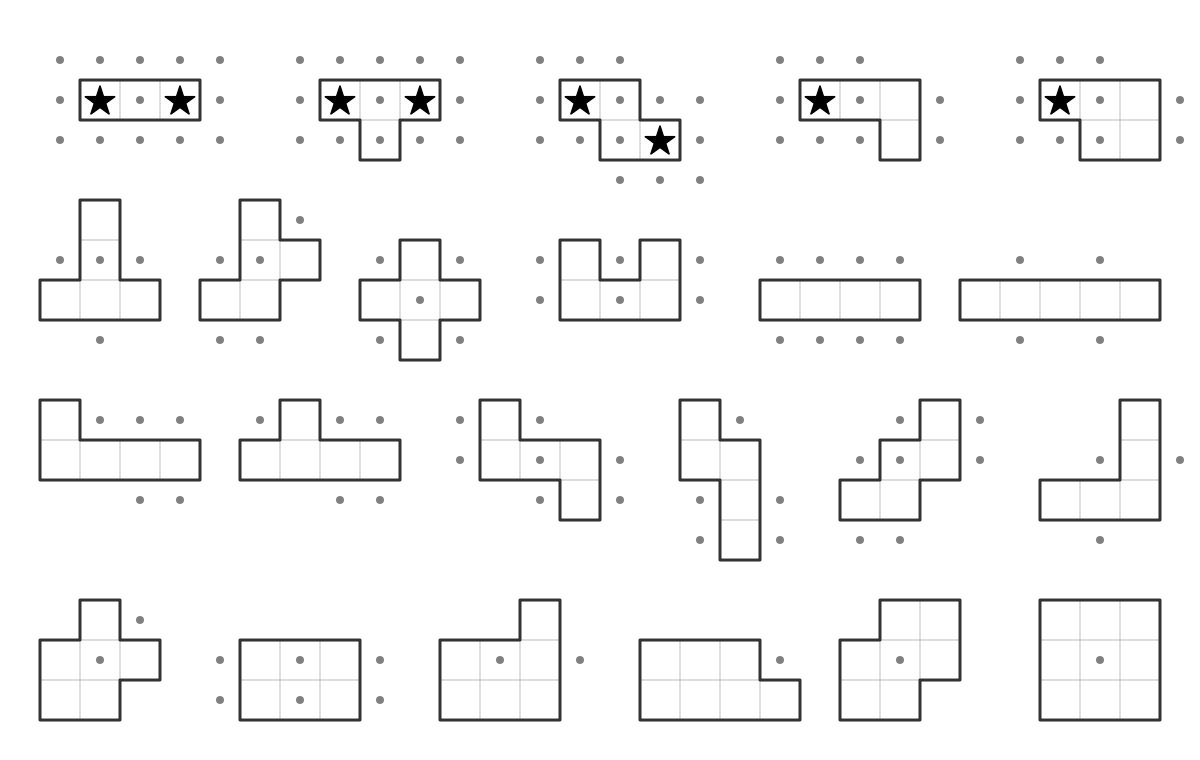
...and the eliminations you can make with these regions, including some that can immediately have stars placed.

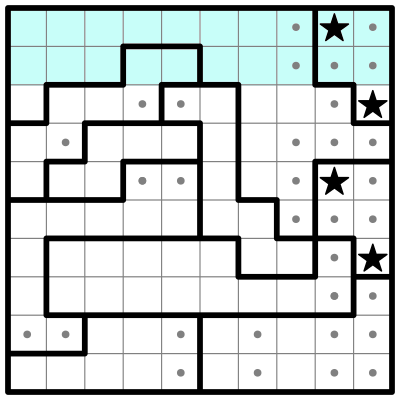
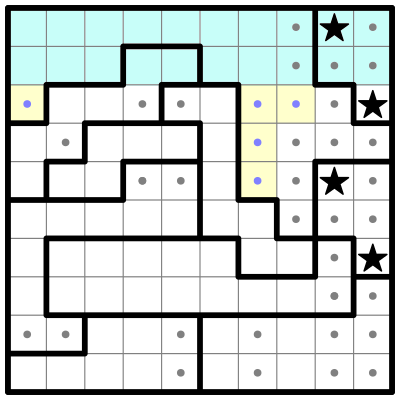
RULE OF CONTAINER CABALS

If two rows are fully occupied by two regions (which also extend outside the rows), then solving the rows would completely solve the regions. All the other squares in those regions — the ones that are not part of the two rows — can be safely eliminated. The regions form a "cabal" which monopolizes the rows.

Conversely, if two regions are fully occupied by two rows which also extend outside the regions, the extra squares in the rows can be eliminated.

This idea can be generalized to any number of rows/columns overlapping any number of regions (as long as the number of each group is the same — you can do it with three rows and three regions, but not with three rows and four regions).

Note that this rule does not work with partially solved containers that already have stars outside the intersection area.

Here's an example puzzle from the Friday, April 24th, 2020 edition of The New York Times. A reader sent me the following partially solved grid: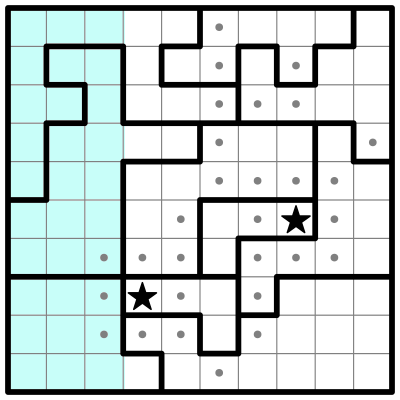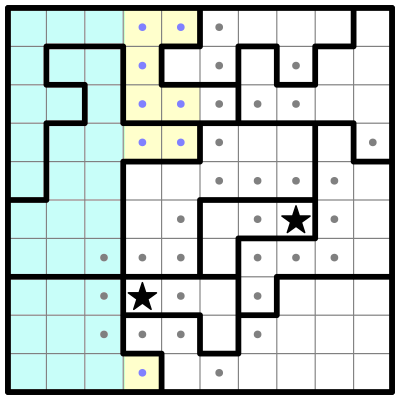

Take a look at the first three columns. You'll see that there are only 3 bolded regions which occupy that space.

By the above Rule of Container Cabals, we can therefore eliminate all the other cells in those 3 containers, like so:

RULE OF CONTAINER CONSUMPTION

This rule applies to 2-star puzzles: If part of a container must make use of at least one star, the rest of the container may contain at most one other star. Seems obvious, no?

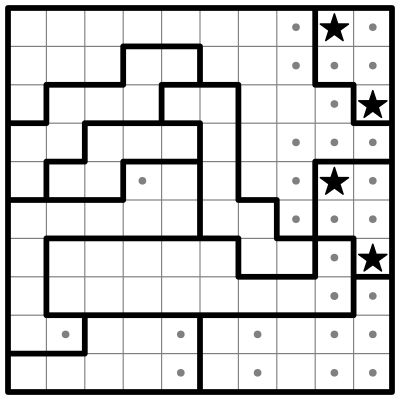
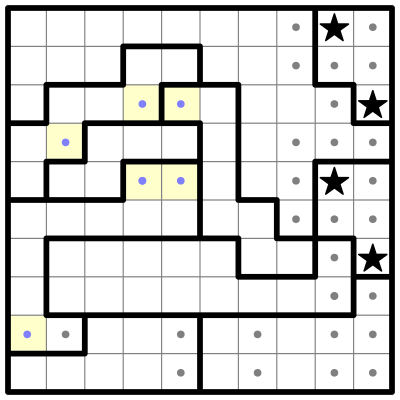
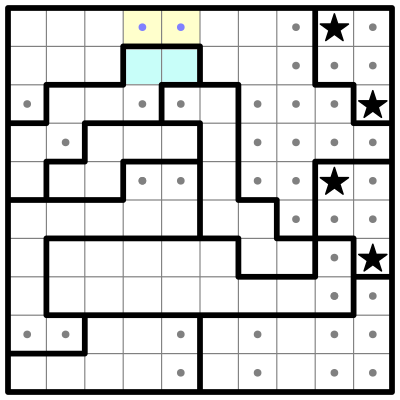
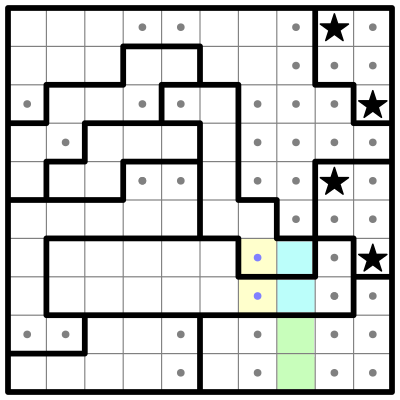
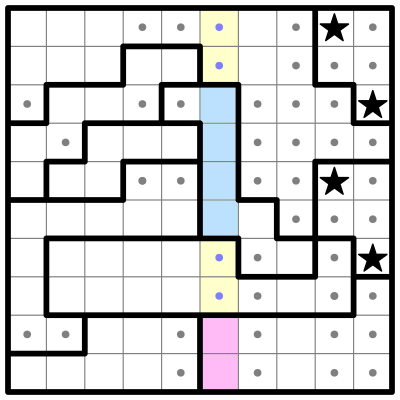
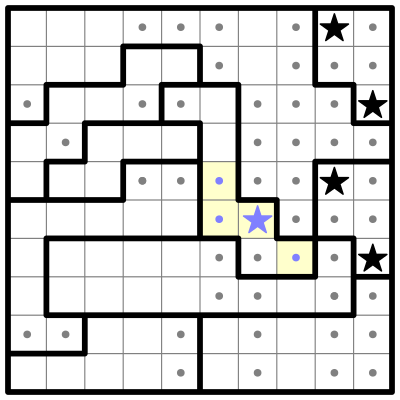
Now I'll combine some of the above rules in this partially solved example from the Saturday, April 25th, 2020 edition of The New York Times:

Using the Rules of Crowding and Four-Squares, we can eliminate the cells that crowd the small region in the center, along with an additonal elimination thanks to the region in the lower left corner.

Now, looking at the first two rows, there is only one star accounted for; by the Rule of Container Consumption, there must be exactly three others.

One must go in the sole open region in row 1. The same Rule tells us that the rest of the region can only contain one other star, and looking at row 2 there are only two bolded regions that can still hold stars at all. One is a two-cell sub-region, which can hold at most a single star, so the other star in row 2 must be in the same bolded region as row 1. This exactly accounts for all four stars in the first two rows, as well as both stars in the top-left bolded region. The Rule of Finished Containers lets us eliminate the remaining cells in that bolded region:

We also know that the two-cell sub-region on row 2 must contain a star, so we can use the Rule of Crowding to eliminate a couple more cells.

Using the Rule of Clumps, I can see where each star goes in column 8, so I eliminate cells in column 7 to prevent them from being crowded out:

Using the Rule of Four-Squares, I can see the pink sub-region (shown below) must contain a star, and the blue sub-region above it must also, or there would be insufficient room in its bolded region. So we can eliminate the remaining cells in column 6.

Now we can place another star in column 7:

And the rest of the puzzle solves easily from here.

Happy puzzling!