January 21st, 2019
Dearest Krazy Dad,
I hope this message finds you well and that your new year is off to a wonderful start! I just made a small donation through PayPal and also wanted to write you a personal message. I was born and raised in the US and during my elementary school years in a “gifted” classroom, we started every day with logic puzzles. I will never forget the fun, challenge, or satisfaction of starting every day tackling a logic puzzle! I now live in India, where I started Kranti NGO, which empowers girls from Mumbai’s red-light areas to become agents of social change. We currently work with 20 girls, ages 13-23 who are daughters of sex workers, survivors of trafficking, or girls born and raised in Kamathipura, one of Asia’s most infamous red-light areas.
In the past five years, Kranti’s girls have: become the first girls from India’s red-light area to study abroad, received UN awards for their social justice work, given 25+ TEDx and other speeches around the world, and written, directed and performed their own play in front of 100K+ audience members. Their latest performance, at the world’s largest performing arts festival in 2017, was covered by BBC with over ten million views. In 2016 Kranti’s alternative school was named a Top 10 for the $1 million Global Teacher Prize, and three Kranti girls are currently studying in universities in Rome, Chicago, and Los Angeles.
Please watch the “Global Teacher Prize” video if you have a few minutes….it will give you an idea of how our curriculum works and why you are such a vital part of it. I’ve been using your worksheets at least 2-3 times a week ever since we started Kranti School in 2014. There are some girls in our home who are completely illiterate and have never been to a mainstream school, but they LOVE your puzzles. The variety of puzzles has really given the girls a chance to see how intelligent they are and that they do love learning…quite a feat for girls who grew up their whole lives hearing from their teachers that “a whore’s daughter can only be a whore.”
As we are an NGO and I do all of the fundraising for Kranti as well as teach school full time, I can’t afford much more than $20, but I will continue to make contributions every time we get an education grant. Your website saves me so much time every week and there’s no amount of money I could possible send you that would be adequate for the amount of energy, passion, and love for learning that you’ve single-handedly brought into our classroom. I hope you’ll take a minute today to appreciate and thank yourself for the thousands of lives you must be touching around the globe without even knowing it. Personally, I’ll just say you’ve made my life as a teacher significantly more fun and manageable!
Lots of love and gratitude,
Robin
Permalink | Comments Off on Mailbag Monday
May 18th, 2018
I was recently talking to another puzzle maven, and the subject of how I measure the demand for specific logic puzzles came up. I’m interested in puzzle demand because it helps inform the choices I make when I add new puzzles to the website. It occurred to me that my methods may not be as widely employed as I had assumed, and it might be worth sharing them. This technique is not just useful for measuring demand for puzzles, but I’ll use puzzles as an example.
If you’re interested in measuring demand, you probably know that Google has a free service called Google Trends which allows you to measure comparative search volume for multiple search terms. One can debate how much Google search-engine demand correlates to “actual” demand (whatever that is), but it seems to me like a reasonable quantifier that is likely correlated (and is simple and easy to obtain). For the rest of the article, I will often use the word “demand” as a placeholder for “Google Search Traffic”.
For example, here’s a chart comparing apples (blue) and oranges (red). Notice there’s a big bump on searches for Apples in the Fall, when they are presumably in season (or maybe people are buying iPhones? I don’t know…).

If I extend the chart over a 5 year period, I can see that the demand for apples and oranges follows a cyclical seasonal pattern – a common phenomenon with many search terms. Apples are popular in the Fall, and oranges in the Winter.
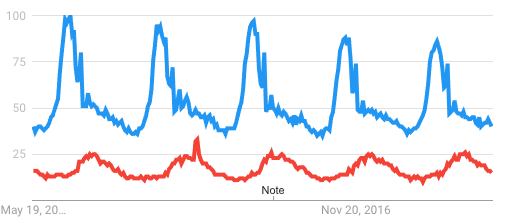
As you can see from these charts, Google doesn’t reveal actual search volume, it only shows relative search volume, which it always maps to a scale from 0-100. Because the numbers are presented as rounded integers, it is not particularly helpful to compare two search terms in which one has 100 times more traffic, because the smaller item will get scaled down to the 0-1 range, which isn’t very informative. For example, if I compare Sudoku (blue) with Slitherink (red), I can’t really learn much about Slitherlink, other than that its search traffic is < 1% of Sudoku, which doesn’t tell me much.

It would be cool if there was a way to measure relative demand for a group of items where several magnitudes separate the most desired from the least desired items. As it happens, there is.
So my “one weird trick” is to use a small stable search term as a baseline (I call this kind of system “pants-rank” for reasons that will soon be clear). Recently, I’ve been using Futoshiki, a relatively unpopular Japanese logic puzzle, as a baseline for measuring search demand for other logic puzzles. So I measure puzzle demand in “F-Units” (or futoshikis, in which the demand for Futoshiki is normalized to 1. So for measuring puzzle demand, Futoshikis are my “inch”.
Here’s the demand for Futoshiki (blue) and Slitherlink (red), two puzzles with similar demand.

On the real chart, if you hover over the “average” bars on the left, you get two integers (again scaled to 0-100) which indicate that Futoshiki has an average relative demand of 61 and Slitherlink has 38.
 So the F-units of Futoshiki are 1 (by definition) and the F-units of Slitherlink are 38/61 (or .62). I can then work my way up to successively more popular puzzles, and work out the F-units for Kakuro (5.38) and Kenken (8.77). Eventually the scaling for Futoshiki becomes too small, so instead I use a known puzzle whose F-Units I’ve already determined as a baseline for measuring more popular puzzles like Sudoku and Crosswords. Using this technique, I’ve worked out that Sudoku demand is at approximately 395 F-units and Crosswords are at a whopping 857 F-units. Here’s a table showing F-Units for a number of puzzles I’m interested in. So the F-units of Futoshiki are 1 (by definition) and the F-units of Slitherlink are 38/61 (or .62). I can then work my way up to successively more popular puzzles, and work out the F-units for Kakuro (5.38) and Kenken (8.77). Eventually the scaling for Futoshiki becomes too small, so instead I use a known puzzle whose F-Units I’ve already determined as a baseline for measuring more popular puzzles like Sudoku and Crosswords. Using this technique, I’ve worked out that Sudoku demand is at approximately 395 F-units and Crosswords are at a whopping 857 F-units. Here’s a table showing F-Units for a number of puzzles I’m interested in.
For what it’s worth, the demand indicated by Google Trends does not necessarily match the demand for puzzles that I see on my website. This is because other factors come into play, like how well I’m ranked on Search Engines, puzzle scarcity, and other intangibles. For example, Suguru is a very popular puzzle on my site, for some reason (in the KenKen/Kakuro range), but doesn’t seem to be hugely popular on Google.
In the past I’ve used this same trick to measure many other non-puzzly things. When I first did this, I used “pants” as my baseline (another fairly stable search term that has a slight bump in the late Fall preceding Christmas), and used them to measure celebrity popularity in “P-Units” (Pants-units). Hence “pants-rank”. “Chairs” is actually a more stable unit as it is less prone to seasonal fluctuations. Here, for example, is Lady Gaga (blue) compared to pants (red) and chairs (yellow) for the past 5 years. The spikes likely correspond to album releases and TV appearances.

I can see that Lady Gaga has been averaging 0.43 P-units and 1.11 C-units over this period (and I also happen to know she is about 435 Futoshikis – about Sudoku level, but not quite Crossword level popularity. But who is, really?
Permalink | Comments Off on Pants-rank: Comparing Apples, Oranges with Google Trends
May 12th, 2018
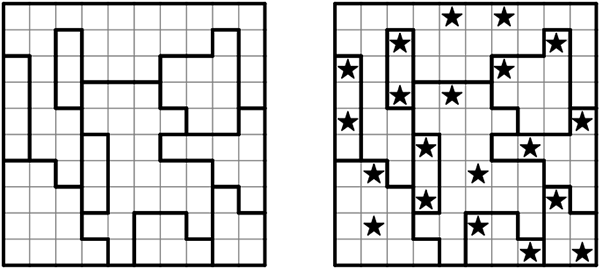
The latest addition to my puzzle menagerie is STAR BATTLE, a newish (well, 21st century, at least) puzzle that was originally created by Hans Eendebak for the 2003 World Puzzle Championship.
If you like Suguru you will probably find these fairly easy to get into, as they are somewhat similar. But instead of placing numbers, you are placing stars – a fixed number of stars in each row, column and bolded region. Like Suguru, the stars may not be adjacent to each other, not even diagonally.
I find these very aesthetically pleasing. I think it has something to do with the stars. If you were placing sturgeon or aardvarks into the puzzle, I don’t think I’d like it as much, but honestly, you can use any symbol you like.
I am currently carrying two versions of this puzzle: 8×8 puzzles that have 1-star in each container, and 10×10 puzzles that have 2-stars. The 10×10 2-star puzzles are significantly harder than the 8x8s.
If you’re new to the puzzles, and find them difficult to get started, then you might find this tutorial I wrote helpful. Or not. Let me know.
Enjoy the puzzles!
STAR BATTLE
Permalink | Comments Off on Star Battle: Oh my gosh they’re full of stars!
April 30th, 2018
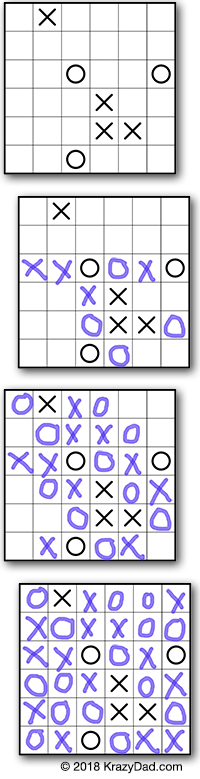 I get a lot of requests for new puzzle varieties (all different kinds) but I started getting a lot of requests for one particular puzzle the past couple of years. I didn’t notice at first, because the different requesters were using different names: Binairo, Tic-tac-logic, Binoxxo, Binario, (I later discovered it is also called Takuzo, Binary Puzzle, Bineiro, Brain Snacks, Unruly, Zinero and Zernero). All names for the same curiously addictive puzzle, sometimes filled with Xs and Os, sometimes with 1s and 0s. Regardless of the symbols used, the rules are the same: I get a lot of requests for new puzzle varieties (all different kinds) but I started getting a lot of requests for one particular puzzle the past couple of years. I didn’t notice at first, because the different requesters were using different names: Binairo, Tic-tac-logic, Binoxxo, Binario, (I later discovered it is also called Takuzo, Binary Puzzle, Bineiro, Brain Snacks, Unruly, Zinero and Zernero). All names for the same curiously addictive puzzle, sometimes filled with Xs and Os, sometimes with 1s and 0s. Regardless of the symbols used, the rules are the same:
- Fill the puzzle with two symbols (like Xs and Os).
- Horizontally and vertically, there can be no more than 2 of the same symbol touching.
- There are an equal number of Xs and Os in each row and column.
- Each row must be unique. Each column must be unique.
Today I am introducing this fun simple puzzle to my collection. I am calling my version Binox — none of the other names seems to be used by more than one publisher, and who am I to break tradition? My version is available in 5 sizes ranging 6×6 to 14×14. I offer four different difficulty levels (Easy, Novice, Challenging and Toughest).
You’ll find both printable Binox puzzles and interactive Binox puzzles here at Krazydad. The interactive puzzles are available in both the X/O format and the 1/0 format (use the gear-icon to change it). For the moment, I’m offering the print puzzles only in X/O, however, if this omission is keeping you up at night, let me know, and I’ll add a duplicate set with 1s and 0s.
PRINTABLE BINOX
INTERACTIVE BINOX
Enjoy the puzzles!
Permalink | Comments Off on Binox Puzzles are here!
March 2nd, 2018
 Celebrity rankings, based on the number of prayer candles for sale on Etsy, 2018 EDITION Celebrity rankings, based on the number of prayer candles for sale on Etsy, 2018 EDITION
1.
Tupac Shakur
2.
Beyoncé
Kanye West
3.
David Bowie
Princess Leia / Carrie Fisher
4.
Dolly Parton
Harry Styles
5.
Britney Spears
Notorious Biggy Smalls
Lana Del Ray
6.
Drake
Kim Kardashian
7.
Leo DiCaprio
Snoop Dogg
Lady Gaga
Kendrick Lamar
Bill Murray
8.
Adele
Bernie Sanders
Donald Trump
Rihanna
RuPaul
Eminem
9.
Hillary Clinton
Morrissey
James Franco
Chance the Rapper
10.
Cardi B
Kurt Cobain
Jimmy Fallon
Justin Trudeau
Permalink | Comments Off on Celebrity Prayer Candle Rankings, 2018
February 22nd, 2018
 I started publishing print-on-demand puzzle books a few months ago, and I’m now up to 22 books. Yay! The latest are four volumes of Killer Sudoku, available in Large Print and 4-per-page. The most popular, at the moment, are the “Tough Kakuro” and the “Stupendous Suguru” books. I started publishing print-on-demand puzzle books a few months ago, and I’m now up to 22 books. Yay! The latest are four volumes of Killer Sudoku, available in Large Print and 4-per-page. The most popular, at the moment, are the “Tough Kakuro” and the “Stupendous Suguru” books.
The easiest way to find my books is to search for “Krazydad” on Amazon.
If you think I’m getting rich from my burgeoning publishing empire, you would be wrong! I make a few dollars per book, and I’m selling about a book a day, which is keeping me in coffee, but not exactly paying for my dog’s chiropractor. If you’d like to help me work my way up to TWO cups of coffee, you can help by reviewing my books (honestly) after you buy them. Thanks!
The print-on-demand company I’m using is CreateSpace which is owned by Amazon. There are rumors that CreateSpace might get merged into Amazon’s very similar KDP (Kindle Direct Publishing) service. If/when this happens, it may affect the availability of my books for a short time, but they should reappear. My reason for not initially publishing on KDP is that it requires that the book be made available in digital form for the Kindle. Since my books require pencils/pens, they need to be on paper, not Kindles. I wouldn’t want Kindle owners buying virtual versions of my books only to be disappointed, and leaving bad reviews.
If you’re curious how this whole self-publishing thing works, and want more gory details, I’m happy to share – just contact me via email.
Permalink | Comments Off on Books, books and more books
December 19th, 2017
 Looking for a little more variety in your daily puzzle consumption? Looking for a little more variety in your daily puzzle consumption?
Gregory Gray wrote to tell me about his indie puzzle magazine, Topple. Each issue costs a buck to download and print yourself, and there is a very wide variety of puzzles, many with illustrations which remind me a bit of the Sam Loyd Cyclopedia, if you know what that is.
Greg is currently up to Issue #7, as of this writing. The latest issue contains 16 puzzles, of which four are Nikoli style puzzles (Masyu, Hashi, Nurikabe, Kakuro) and the others are from further afield. I very much like the anagram ring puzzle shown here.
Here’s a sampler that Greg sent me.
And here’s the website where you can get more!
Permalink | Comments Off on Topple puzzle magazine
June 22nd, 2017
I sometimes get emails that ask where the logic puzzles are. “I thought your site had logic puzzles, where are the logic puzzles?” they ask.
My site does indeed have logic puzzles, by which I mean puzzles in which you employ logic to solve them. Pretty much every puzzle on my site meets this description. However, I’m being pedantic. I believe the logic puzzles being referred to by my correspondents are the kind that involve a group of girl scouts, sitting at a counter in a Boba shop, each with a different skill badge, a different pet, and a different beverage:
The 7 year old sits on a red stool.
The 8 year old has a schnauzer.
The 9 year old is drinking a green tea boba.
The green stool is just to the left of the white one.
The girl on the green stool is drinking a mocha boba.
The girl with the computer-expert badge has a one-legged parrot.
The girl on the yellow stool has a dancer badge.
The girl in the center is drinking a strawberry boba.
The 11 year old is on the first stool.
The girl with the hiking badge is next to the girl with an ocelot.
The girl with the pottery badge is drinking taro boba.
The girl with the magical pony is next to the dancer
The 12 year old has a home scientist badge.
The 11 year old is next to the girl on the blue stool.
The hiker is next to the girl drinking a plain tea boba.
Who’s got the Ferret?
Although these are commonly called logic puzzles, I prefer to call them “logic word puzzles”, since there are all kinds of puzzles that employ logic, not just these. I’ve also seen them called Einstein’s Puzzle, also a terrible name.
Whatever they are called, I don’t carry them. This is because of those pesky words. In order to produce them, I would have to come up with 4-6 lists of related things (girl scouts, boba beverages, sweaters, mood-rings, troll figurines, etc.) for each individual puzzle, and this would be extremely labor-intensive, especially since I like to put out many thousands of each puzzle variety, so you don’t run out.
This website currently has over a million puzzles on it, and the reason there are so many is because I’m able to use power tools (namely, computer programming) to produce them. I’ve thought about combining various word lists in combinatorial ways to produce these puzzles, but I don’t think the results would be very appealing (there are five girl scouts, each has a favorite muscle car, lives on a different planet, and has a different number of legs). Probably the best solution would be for me to crowd-source the word lists. The idea being that you, the visitors to this website, could suggest lists of things to use in puzzles), but setting this up would also be very time consuming, and would probably require moderation so as not to be abused by spammers and trolls.
For similar reasons, I don’t carry Fill-a-pix, Mosaik, Connect-the-dots, and other puzzles that employ unique pictures for the solutions, not to mention Word-Search and Crosswords. If you want to set up a moderated crowd-sourcing system for word-puzzle and picture-puzzle content that I can use, let me know when it’s running! I’d love to use it!
Permalink | 2 Comments »
March 1st, 2017
 Hey folks, I’m currently working on a series of puzzle books which will be available on CreateSpace and Amazon, starting sometime in March, 2017. [ UPDATE: They’re available! ] Hey folks, I’m currently working on a series of puzzle books which will be available on CreateSpace and Amazon, starting sometime in March, 2017. [ UPDATE: They’re available! ]
I’m starting with a Suguru collection. Each Suguru book contains 300 puzzles and is priced at $9. The puzzles in the books are all new, and do not appear on the website. Learning how to self-publish has been (and will continue to be) an interesting journey. I had a lot of fun figuring out how to make a book cover that uses the Droste effect.
After Suguru I’ll be working on books of Kakuro, Krypto Kakuro, Killer Sudoku and more. If there’s a particular puzzle variety you’d really like to see in book form, let me know!
I’d love to include a variety of short testimonials from actual Krazydad visitors, like yourself, on the back cover. If you’d like to submit a short testimonial, drop me an email with the subject line “Krazydad Testimonial”, and let me know how I should credit you (e.g. “Jane from Pittsburgh”). By sending the email, you are tacitly agreeing to let me publish your testimonial on one or more back covers.
Also, if you’d like to receive (very occasional) announcements by email, when I publish new books, let me know!
Thanks so much!
UPDATE: My first Kakuro books are now available on CreateSpace.
UPDATE: My first volumes of Easy and Challenging Suguru puzzles are now available on the CreateSpace store, as well as on Amazon. Enjoy!
Permalink | 7 Comments »
February 28th, 2017
Part 7. Through the Looking Glass
This is one of a series of posts about my health/fitness journey. The first one is here.
It’s been a while since I’ve written one of these, so here’s a quick update. It’s late February, 2017. I’ve been hovering around 180 pounds (plus or minus 3 pounds) since early November, last year. This is a good thing in that I’ve been able to maintain a healthy weight for several months, and I’m not experiencing diet fatigue (a big problem for me the last time I made it down this far). I’d like to be a few pounds lighter, but I’m very happy with the weight I’m at, especially considering I was at 245 a year ago.
I’m the most fit I’ve been in, well, ever. Certainly since I was in my early 20s, and even then I never exercised. Now I’m going to the gym 4-6 days a week, and I can see the effects in the mirror.
 When I was a kid, I was fascinated with mirrors. We had a big floor-to-ceiling mirror in our living room, when I was growing up, and I liked to play with it. Early on I discovered the trick of making spiders or crabs, by sticking my hand out on the edge of the mirror, and exploiting the symmetry. A friend and I would stand on opposite ends of the mirrors in department stores, bisecting our bodies as evenly as possible to make it look like we had three legs, or were floating in the air. When I was a kid, I was fascinated with mirrors. We had a big floor-to-ceiling mirror in our living room, when I was growing up, and I liked to play with it. Early on I discovered the trick of making spiders or crabs, by sticking my hand out on the edge of the mirror, and exploiting the symmetry. A friend and I would stand on opposite ends of the mirrors in department stores, bisecting our bodies as evenly as possible to make it look like we had three legs, or were floating in the air.
And very early on, I discovered some of the laws of mirrors. For example, I noticed that if you looked at someone’s reflection in the eyes, then they would see that your reflection was making eye-contact with them. And the corollary of that: if you can see someone’s eyes in a mirror, then they can see you.
I remember looking in the mirror at the age of six or seven, and imagining what my future adult self would look like. I imagined an older single man, with the same bowl haircut and bangs, his house filled with boxes of the froot loops my mom wouldn’t buy (too much sugar!). As I grew into my adolescence, and got more into music, I would look in the mirror and imagine my future album covers, posing as a serious brooding rock star.
I found mirrors more troublesome in my twenties. I remember a Mexican restaurant near my work that had a wall of mirrors. I found that if I sat facing the mirrors, it was difficult for me to concentrate on what my colleagues were saying, because I would be distracted by my reflection. I learned to sit with my back to the mirror.
And as I continued to age, that distraction became more unpleasant. I stopped wearing bangs pretty quick, and pretty soon, by my early 30s, I lost a lot of my hair. My dreams of being a cereal-eating guy with bangs were dashed! The slight double-chin I had developed in my late teens became more and more pronounced, and I grew a beard to cover it. As I grew into my thirties, forties and fifties, the act of looking at myself for long periods in the mirror became a distant memory. The occasional Hitchcockian glimpses of the mirror became almost frightening – reminders that I wasn’t the abstract cereal-eating child in my head, but a physical creature, mortal, fat and frail.
It had been so long since I was at a healthy weight that I thought I had created a permanent condition. The fat on my belly had become a big hard slab. The idea of reversing or easing my condition seemed like an insurmountable wall. At 53, I thought I had probably abused my body so much, that I was basically done; just watching the clock until the end. Of course, I didn’t allow myself to think about this very much; I spent most of my time (as I still do) “in my head”. But, I was far more distressed than I allowed myself to realize.
And of course, there was that whole “endomorph” thing. Based on my conversations with others, and my reading, I had classified myself as an “endomorph”. It was the equivalent of Cartman on South Park insisting he is “big boned”. I was endomorphic, that’s the body type I had, and there was no changing it. I wished I was an ectomorph, but you get the genes you’re dealt, or so I thought.
So now, I can say, with the benefit of hindsight, that the whole endomorph/ectomorph thing is pure and utter bullshit. When I first met a nutritionist I was working with, last year, she told me confidently I was an endomorph. A few months and about 30 pounds later, I asked her, “if I came in for the first time today, what would you classify me as?” “A mesomorph” she said.
So was I fat mesomorph? Am I now a skinny endomorph? No. I reject the whole notion. To paraphrase Popeye, I yam what I yam (which is mostly yams, if it’s Thanksgiving).
If you have only a passing familiarity with the terms ectomorph, endomorph, and mesomorph. I suggest you read the wikipedia article about William Herbert Sheldon, the doctor who invented “somatotypology” back in the 1940s. He published volumes of nude photographs of young men and women, with very precise descriptions of their body types, and it is very clear, from reading his actual work (I bought his 1954 book “The Atlas of Men” on EBay) that the guy was an utter quack. It is also quite possible, by the way, that nude photos of Bill and Hillary Clinton are included in his photos of Yale students which are sealed at the Smithsonian!.
While it might be useful to use somatotypological language to discuss the state that a body happens to be in at the moment these terms should definitely not be used to describe a permanent state-of-being from you which cannot recover. Any health professional who casually uses those terms to describe you is participating in a form of pseudo-science, not much different than astrology or phrenology.
So at the moment, I look at the mirror again, after all these years, without fear or disgust. I can see that I am not an endomorph, ectomorph or mesomorph. I am me. It is certainly clear that I have some issues which are different than you, different than some of my skinny friends who seem to be able to consume vast quantities of beer and fried foods. My issues aren’t really with my body type. They are with my relationship with food. I know that if there is a plate of cookies in the house, I am going to be thinking about that plate of cookies, nearly continuously until the plate of cookies is gone. I know that if I have a plate of food in front of me, I’m going to finish it. Those issues are pretty much the same as they were a year ago. What is different is how actively I am working to prevent those issues from running me into the ground.
My frequent visits to the gym are a huge part of this. Let’s be clear: the exercise is not having much of an effect on my weight loss. I cannot lose weight simply by exercising more. But it has a massive effect on my energy levels, my positive outlook, and my muscle tone. I have regained some of the narcissism of my youth, actually enjoying periodically gazing at my biceps in the mirror, trying on clothes, looking at them — something I thought I would never do.
And I’ll allow myself a little narcissism at this point. I’ve been on the other side of the mirror.
Permalink | Comments Off on Through the Looking Glass
|
|





 So the F-units of Futoshiki are 1 (by definition) and the F-units of Slitherlink are 38/61 (or .62). I can then work my way up to successively more popular puzzles, and work out the F-units for Kakuro (5.38) and Kenken (8.77). Eventually the scaling for Futoshiki becomes too small, so instead I use a known puzzle whose F-Units I’ve already determined as a baseline for measuring more popular puzzles like Sudoku and Crosswords. Using this technique, I’ve worked out that Sudoku demand is at approximately 395 F-units and Crosswords are at a whopping 857 F-units. Here’s a table showing F-Units for a number of puzzles I’m interested in.
So the F-units of Futoshiki are 1 (by definition) and the F-units of Slitherlink are 38/61 (or .62). I can then work my way up to successively more popular puzzles, and work out the F-units for Kakuro (5.38) and Kenken (8.77). Eventually the scaling for Futoshiki becomes too small, so instead I use a known puzzle whose F-Units I’ve already determined as a baseline for measuring more popular puzzles like Sudoku and Crosswords. Using this technique, I’ve worked out that Sudoku demand is at approximately 395 F-units and Crosswords are at a whopping 857 F-units. Here’s a table showing F-Units for a number of puzzles I’m interested in.


 Celebrity rankings, based on the number of prayer candles for sale on Etsy, 2018 EDITION
Celebrity rankings, based on the number of prayer candles for sale on Etsy, 2018 EDITION


 When I was a kid, I was fascinated with mirrors. We had a big floor-to-ceiling mirror in our living room, when I was growing up, and I liked to play with it. Early on I discovered the trick of making spiders or crabs, by sticking my hand out on the edge of the mirror, and exploiting the symmetry. A friend and I would stand on opposite ends of the mirrors in department stores, bisecting our bodies as evenly as possible to make it look like we had three legs, or were floating in the air.
When I was a kid, I was fascinated with mirrors. We had a big floor-to-ceiling mirror in our living room, when I was growing up, and I liked to play with it. Early on I discovered the trick of making spiders or crabs, by sticking my hand out on the edge of the mirror, and exploiting the symmetry. A friend and I would stand on opposite ends of the mirrors in department stores, bisecting our bodies as evenly as possible to make it look like we had three legs, or were floating in the air.